|
| Når lysningen i hullet er s [m2] så er flowet q=v×s [m3/S] |
Beregningen af flow baseres dels på en teori og dels på praktiske observationer. Teorien er meget enkel og er formuleret af Torricelli. Den siger at farten af en udstrømmende væskepartikel i et kar gennem et hul som sidder H meter under overfladen er den samme som væske partiklen ville have fået ved et frit fald på H meter.
|
|
| Når lysningen i hullet er s [m2] så er flowet q=v×s [m3/S] |
Torricellis lov kan anvendes til at beregne flow i
overløb. Det enkleste at beregne er flow i et overløb med
en rende af form som et rektangel. Renden tænkes delt op i mange
tynde vandrette snit. For hvert af disse snit kendes højden
under overfladen. Den er H-x [m]. Lysningen på åbningen
hvorigennem væsken løber ud er B×dx [m2].
Ved anvendelse af Torrecellis lov kan
væskestrømmen i det tynde lag: dq beregnes.
Væskestrømmen igennem hele
tværsnittet får man ved at summere strømmen igennem
alle de vandrette
snit. Når tykkelsen af de vandrette snit går mod nul
så
bliver denne summation til en integration over hele opstuvnings
højden: H
 |
 |
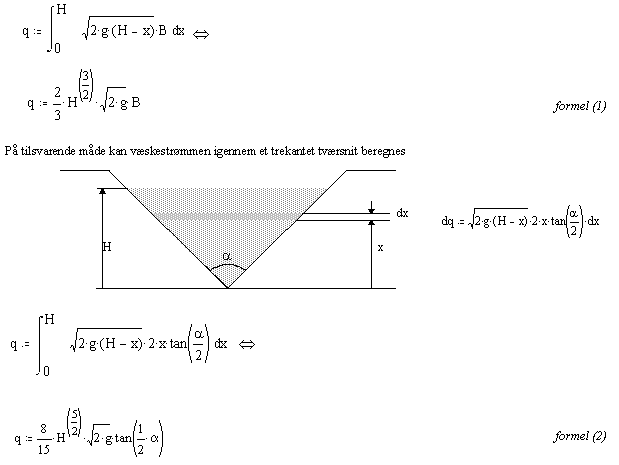Beregningerne gælder ved laminær strømning (ikke turbulent) i overfaldet. Hvor intet andet nævnes tales der om skarpkantede overfald.
Formlerne 1 og 2 giver et godt mål for strømningen selv om formlerne er simple. En af manglerne ved formlerne er at de kun tager tyngdekraftens påvirkning af væsken i betragtning. Der er naturligvis andre kræfter der spiller ind. Først og fremmest er det gnidnings kræfter internt i væsken og mellem væsken og de flader og kanter den bevæger sig imod.
Væskens masse betyder også noget andet end at tyngdekraften trækker væsken mod jorden. Den betyder nemlig at væskens inerti vil modvirke retningsændringer i strømningen. Dette ses tydeligt på forskellen mellem strømmen igennem et rektangulært overfald med sidekontraktion(figur 2) og strømmen igennem et rektangulært overfald uden sidekontraktion(figur 1).
Endelig er der overfladespændingen, som betyder noget ved meget små opstuvninger og ved meget små overfald, så små, at de nok ikke har nogen praktisk betydning.
Til at imødegå de forhold, som ikke dækkes af teorien anvendes impiriske korrektioner.
Alle korrektioner, der omtales her er faktorer til formel 1 eller formel 2 henholdsvis. De anvendte faktorer er mere eller mindre komplicerede funktioner af overfaldsbygværkets geometriske mål. Den enkleste er blot en konstant.
I litteraturen ser korrektions faktorene umiddelbart forskellige ud, men ved nærmere eftersyn viser de sig at være ens indenfor to eller tre cifre.
Rektangulært overfald uden sidekontraktion: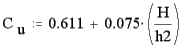
| Væske strømmen for denne type overfald er således: |  |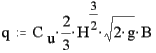
formel (3) |
hvor
| H | er | opstuvnings højden |
| B | er | overfaldskantens længde |
| h2 | er | overfaldskantens højde over kanalens bund |
| g | er | tyngde accelerationen |
Der er knyttet nogle forudsætninger til formel 3:
| 1: | H < 2×h2 | |
| 2: | H ≤ 2×h3 AND h3 ≥ 0.3 [m] | hvor h3 er højden på det fri fald efter overløbskanten |
| 3: | L ≈ 4×H | hvor L er den vandrette afstand fra niveaumåleren til overløbskanten |
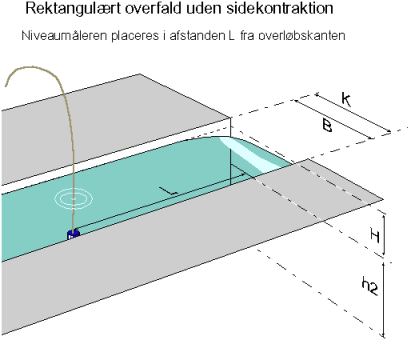figur1 
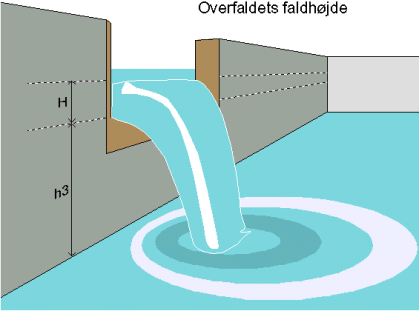figur3Korrektionen er en faktor, som består dels af
Cu, der også bruges når der ikke er sidekontraktion og dels
af en faktor, der reducerer overløbskantens længde i
forhold
til den fysiske værdi.
Rektangulært overfald med sidekontraktion:
| Væske strømmen for denne type overfald er således: |  |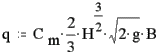
formel (4) |
| H | er | opstuvnings højden |
| B | er | overfaldskantens længde |
| h2 | er | overfaldskantens højde over kanalens bund |
| g | er | tyngde accelerationen |
Der er knyttet nogle forudsætninger til formel 4:
| 1: | H < 2×h2 | |
| 2: | H ≤ 2×h3 AND h3 ≥ 0.3 [m] | hvor h3 er højden på det fri fald efter overløbskanten |
| 3: | L ≈ 4×H | hvor L er den vandrette afstand fra niveaumåleren til overløbskanten |
| 4: | H < 5×B | (ellers bliver Cm≤ 0 ) |
Der er tale om sidekontraktion når K > B. se figur 2:
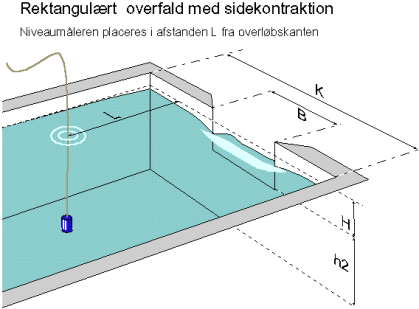figur 2Trekantet overfald: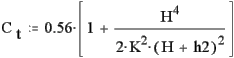
| Væske strømmen for denne type overfald er således: |  |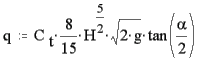
formel (5) |
hvor
| H | er | opstuvnings højden |
| α | er | vinklen mellem overfaldets sider |
| K | er | kanalens bredde |
| h2 | er | overfaldskantens højde over kanalens bund |
| g | er | tyngde accelerationen |
Der er knyttet nogle forudsætninger til formel 5:
| 1: | L ≈ 4×H | hvor L er den vandrette afstand fra niveaumåleren til overløbskanten |
| 2: |  |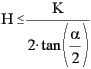
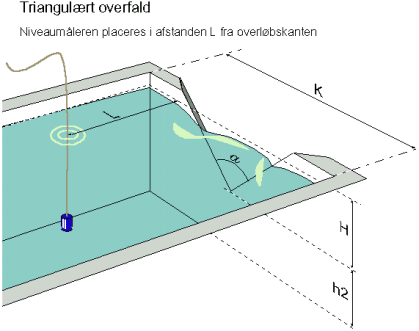figur 4Regne eksempel, rektangulært overfald |
 |
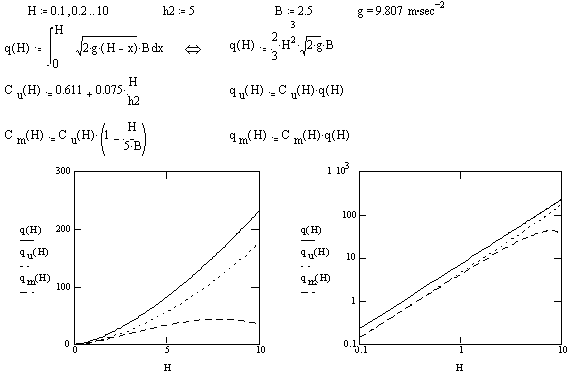| Eksempel på korrektionernes betydning for beregning af strømning i det rektangulære overfaldsbygværk. q(H) viser strømningen uden korrektion, qu(H) viser strømningen med korrektion for et overfaldsbygværk uden sidekontraktion og qm(H) viser strømningen med korrektion for et overfaldsbygværk med sidekontraktion |
Regne eksempel, trekantet overfald |
 |
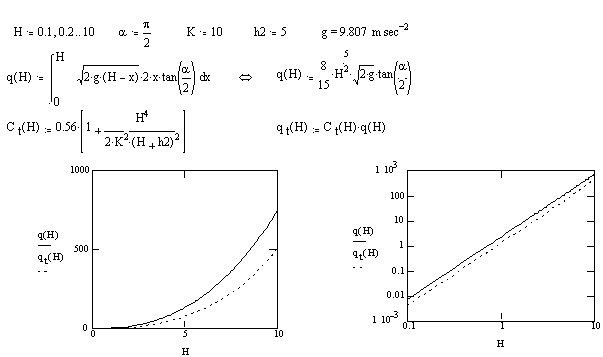| Eksempel på korrektionens betydning for beregning af strømning i det triangulært overfaldsbygværk. q(H) viser trømningen uden korrektion, qt(H) viser strømningen med korrektion. |
Alle enheder skal være fra et afstemt enhedssystem det vil sige mksa eller cgs systemerne. I mksa systemet måles længder i meter[m], masser i kilogram[Kg], tid i sekunder[S] og elektrisk strøm i amperer[A]. I dette system bliver resultatet af de her opgivne formler for væske strøm i [m3/S].
Målingen er specifik for
hver enkel udformning af kanalen. Det vil sige at man køber
beregningen sammen med kanalen. Som eksempel omtales Khafagi venturi
kanalen.
Væske strømmen for denne type
kanal er:
hvor
| H | er | opstuvnings højden |
| B | er | kanalens bredde opstrøms |
| q | er | væskestrømmen i [liter/S] |
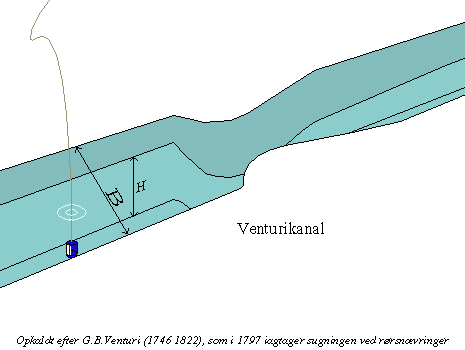figur 5
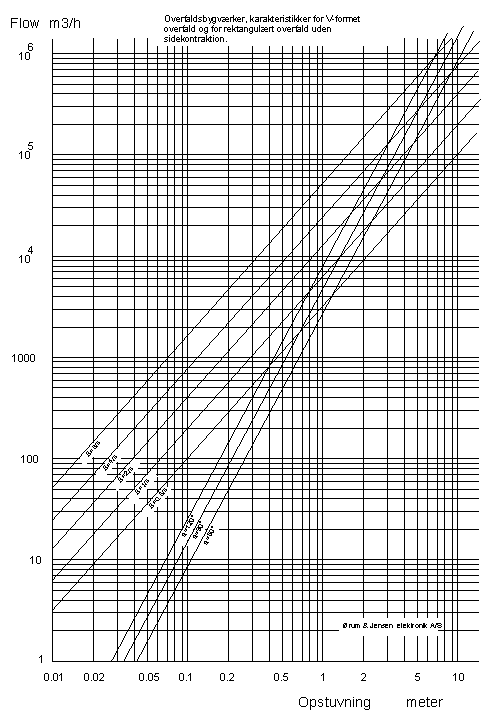
Karekteristikker for begge disse typer bliver rette linier når de afbildes på dobbelt-logaritmisk papir. Den eneste forskel er liniernes hældning. For det rektangulære overløbs vedkommende bliver hælningskoefficienten = 1,5 og for det trekantede overløb bliver den = 2,5. Den interesserede kan overbevise sig om rigtigheden af disse påstande ved at tage logaritmen på begge sider af lighedstegnet i formel (1) henholdsvis formel (2)
